Toothpick polyhedra, fullerenes
Today I bought two 3×150 toothpick packs for 1€ each (in German 1€ shop), or 2.11$ in total. That gives me 900 edges for polyhedra.
So I searched printables.com and found @jmckeand's "Polyhedron Connectors" models:
https://www.printables.com/model/179841-polyhedron-connectors 
I printed single connector on my Prusa MINI+, and that was fine. Toothpicks did fit perfectly.
So I placed 20 of them for dodecahedron (C20 fullerene) with PrusSliceer and created attached 5:18h Prusa MINI+ .gcode (only change I made to DodecConnector.scad was setting Rod_Depth to 1mm for the toothpicks I bought) .
I had to cancel print two times early,
third time worked better. For some pieces adhesion was not good on all 3 corners, and in those cases the holes were a bit too small. A sub millimeter screwdriver helped to get the rod sockets clean. Assembling was not difficult (not easy either). 3Dprinted with new Prusa Orange PLA:
Dodecahedron is C20 fullerene, with 12 pentagons. All fullerenes consist of pentagons and hexagons only. Since they are polyhedra, they are planar graphs as well, and because of that a fullerene always contains exactly 12 pentagons, with all other faces being hexagons.
I want C60 (football) Buckminster fullerene. Thanks to OpenSCAD the 6-6-5 connector needed 60 times should be doable.
I am creating "planar graph playground" (JavaScript for browser/nodejs PostScript, and Python PostScript/Mathplotlib) that displays C20, C30, ... C70 fullerenes as planar convex straight line drawings sofar, with plan of displaying 3D as well. I would not have thought that I would see dodecahedron in analog 3D first 😉
https://hermann-sw.github.io/planar_graph_playground/
This demo is on C30 fullerene, as convex face planar straight line drawing in browser.
Animated .gif demonstrates interaction capabilities selecting edges redraws with that edge as top right edge, dual graph, ... 
I published planar graph playground repo with MIT license, so you can do whatever you want with it. It is still under quite active development.
I borrowed the concept of a "planar face traversol visitor" from Boost graph library.
Especially with JavaScript anonymous functions very compact code does cool stuff.
These 11 lines of code do show color vectors in direction of edge traversal, during planar face traversal, each with a different color:
This is screenshot of Ghostview (gv) displaying the generated Postscript file:
RE: Toothpick polyhedra, fullerenes
I was in same store again, and saw colorful paper drinking straws; bought 100 for 3€ (3.11$) which is 13.5× the price of toothpick per polyhedra edge.
It took way too long to create OpenSCAD connection that can be printed easily on my Prusa MINI+ and really works with 5.65mm inner diameter. Far too late (early) here, model details after some sleep, just a photo of 197mm paper drinking straw dodecahedron next to 63mm toothpick dodecahedron:
RE: Toothpick polyhedra, fullerenes
I published the model with files, photos and design decisions on printables.com:
https://www.printables.com/model/204151-paper-drinking-straw-dodecahedron-connector
0.2mm radius reduced radius of bottom connector compensates for what is left even after using pliers to remove brim.
This is how 20 connector print looks like with brim for my Prusa MINI+:
RE:
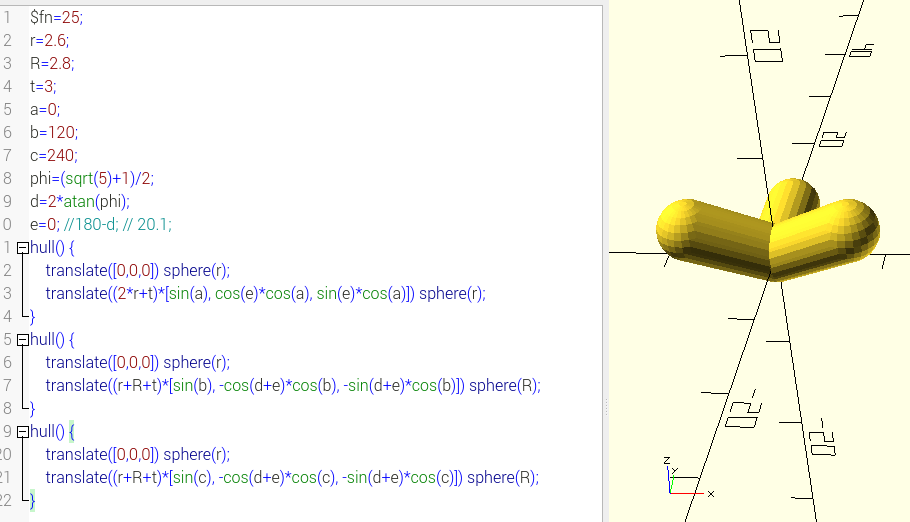
inner diameter of paper drinking straw was 5.65mm, so I chose R=2.8 and r 0.2mm reduced for bottom connector with brim.
In OpenSCAD t is the length of cyclinder part between the sqheres connected with "hull()" function.
a, b and c are the single plane angles of the three connectors.
"dihedral angle" of regular dodecahedron is 2*arctan(phi) with phi being the golden ratio.
https://en.wikipedia.org/wiki/Regular_dodecahedron#Properties
RE:
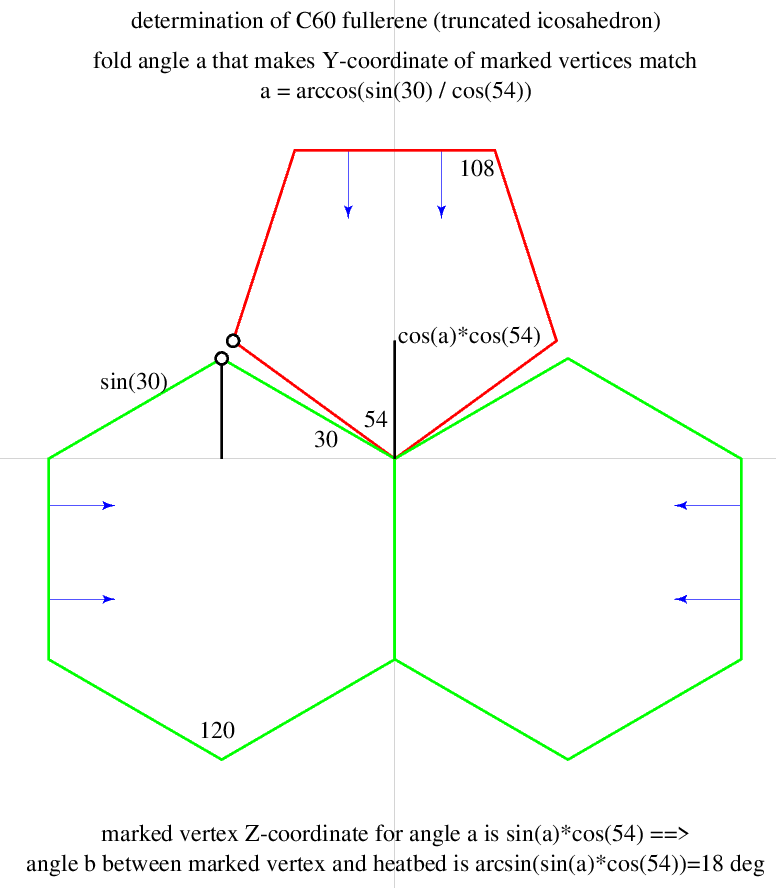
I determined the angle for folding up pentagon joining two hexagons [acos(sin(30)/cos(54)), details later].
I used new OpenSCAD file c60.scad to export c60.stl.
https://www.printables.com/model/204151-paper-drinking-straw-dodecahedronc20truncated-icos/files
With PrusaSLicer I placed 30 C60 connectors, so the .gcode file needs to be 3Dprinted two times.
This is result of print:
Before printing I determined angle between connector into the air and heatbed, and that was exactly 18°.
Because I had made good experience with 20° stairway to heaven before, I did try 18% and it worked.
On Wikipedia I found net representation of C60:
https://en.wikipedia.org/wiki/Truncated_icosahedron
The 100 paper straws have six colors red/yellow/purple/pink/light green/light blue, 16 or 17 of each color.
I decided to use 15 paper straws of each color, and to color same number pentagons with same color from red/yellow/purple/pink, and use the remaining 30 paper straws for connecting:
After printing, removing 60× brim, I assembled the connectors with 90 paper straws.
I did not calculate height before, 197mm long paper straws result in 92cm height, is nearly as high as grand piano:
Now this is big, and question was where to put it.
It is nice having rooms under roof that go up from 2.38m height to above 4m.
A single nail with hook allows to hang C60 at wall and use unused sofar space:
RE:
I determined the angle for folding up pentagon joining two hexagons [acos(sin(30)/cos(54)), details later].
This was the extreme overhang (20°) "stairway to heaven" I had in mind:
https://forum.prusa3d.com/forum/english-forum-general-discussion-announcements-and-releases/supportless-overhang-70-pla-printed-spring-stability-expected/#post-583552 
Here the calculation of pentagon fold angle 31.72° and overhang over heatbed 18°, visualized in Postscript file calc60.ps gist:
https://gist.github.com/Hermann-SW/c5151eddcb8a1271fc5a539e57a1f869
RE: Toothpick polyhedra, fullerenes
I bought "the same" 100 paper drinking straw box today, and tried to modify the 92cm high C60 to have 6 red and 6 yellow pentagons.
This did not work, since the new paper straws have slightly less inner diameter, only 5.5mm.
Perhaps 3Dprinting the 60 connectors again for 5.4mm instead of 5.65 millimeter diameter will work for both types of straws.
But I doubt that 5.65mm inner diameter straws will sit firm enough on new connectors.
The filled faces in below convex face planar straight line drawing of C60 are the 12 pentagons each fullerene has:
https://hermann-sw.github.io/planar_graph_playground/
The red/yellow/purple/pink straws of C60 are the 12 pentagons:
RE: Toothpick polyhedra, fullerenes
I wanted to try with longer edges.
Cheapest 1m edge I found in construction store, that was stiff enough, was M6 threaded bar (1.50$/edge).
I printed 4 of @jmckeand's TetrConnector.scad:
https://www.printables.com/model/179841-polyhedron-connectors/files
- Rod_Diameter 0.585 (cm, measured)
- Rod_Depth 0.5 (cm)
- kept Wall_Thickness as 0.1cm
- exported as STL
- imported into PrusaSlicer
- added 3 duplicates
- clicked on "arrange" I learned about from older son last weekend
- sliced with "brim" and 15% infill (quality), PLA
Worked like a charme after 1:02h printing time, found more "free space" for tetraeder at wall above room door, next to C60 truncated icosahedron. Again single nail with hook was all that was needed to fixate tetrahedron:
RE: Toothpick polyhedra, fullerenes
Back to 60 vertices C60 fullerene, which I had paper drinking straw connectors for.
I created toothpick connectors by slightly modifying OpenSCAD file.
No "hull()" around spheres at start and end anymore, but using OpenSCAD "cylinder()" and "difference()".
I had determined angle to fold the pentagon above as:
d = arccos(sin(30°) / cos(54°))
I had to get used to OpenSCAD "rotate()", and that it allows to specify the axis for rotation.
With that, after rotating by angle d, the 2nd rotation for the two pentagon edges is trivial, just 108°/2=54° in one or the other direction:
translate([0,0,0]) rotate(-90+d,[1,0,0]) rotate(54,[0,1,0]) cylinder(r=R,h=r+t);
With 2nd same function besides the chosen radius (R is 1mm greater than r) in difference(), free space for toothpick gets created centered:
difference() {
translate([0,0,0]) rotate(-90+d,[1,0,0]) rotate(-54,[0,1,0]) cylinder(r=R,h=r+t);
translate([0,0,0]) rotate(-90+d,[1,0,0]) rotate(-54,[0,1,0]) cylinder(r=r,h=r+t);
}
Final added center sphere provides a same distance stop for toothpicks for all three legs:
translate([0,00]) sphere(r);
I created a new model with all files and information:
https://www.printables.com/model/208769-toothpick-c60-fullerenetruncated-icosahedron-conne
Just learned about printables.com X-ray mode of its 3D viewer, that allows to see the hidden center sphere:
When done removing 60× brim and constructing C60:
New C60 on top of 2.10m high storage rack, next to C20:
RE:
The toothpick model worked because of gravity.
The length of toothpick cone part is 9mm, so with t=10 from c60.scad there is only 1mm of contact between non-cone part of toothpick and connector leg. When grabbing toothpick C60 at top and trying to lift it, it falls apart. Perhaps t=12 or t=13 will allow to grab and lift without falling apart.
While single nail with hook seemed to be a good idea to fixate paper drinking straw 92cm high C60 fullerene (truncated icosahedron) at wall shown above, over time gravity did a great deformation. After hanging at ~3m high screw hook, top edge does not even touch ceiling! Lowest point 25cm above my head … the C60 connector for paper drinking straw has 3mm of possible contact with paper straw, which allows to keep all parts together without any glue:
RE: Toothpick polyhedra, fullerenes
New C60 on top of 2.10m high storage rack, next to C20:
I used same cylinder based C60 connector for square matches, so overall model got smaller. It was more work than with toothpicks, but connections were stronger; details added to model:
https://www.printables.com/model/208769-toothpickmatch-c60-fullerenetruncated-icosahedron-

RE:
Lately I played with gdownton's "Polygons to Polyhedrons and More - 30mm Sides" models:
https://www.printables.com/model/167146-polygons-to-polyhedrons-and-more-30mm-sides/comments
After 37.5 hours(!) total 3Dprint time, I built a 438g C60, with 180 magnetic balls holding everything together:
I replaced one orange PLA hexagon with initial test white PETG hexagon, into which I had dremeled two holes for fixating a wire. The whole C60 hangs happily, and even turns smoothly around, see this short youtube video:
Finally 30mm edge length C60 joins 1m edge length tetrahedron:
P.S:
Many different polyhedra can be build with the polygons, here 8 hexagon and 12 pentagon C36-
Middle 6 hexagon ring consists of faces 1+2+4+6+8+10 in C36.1 graph right: 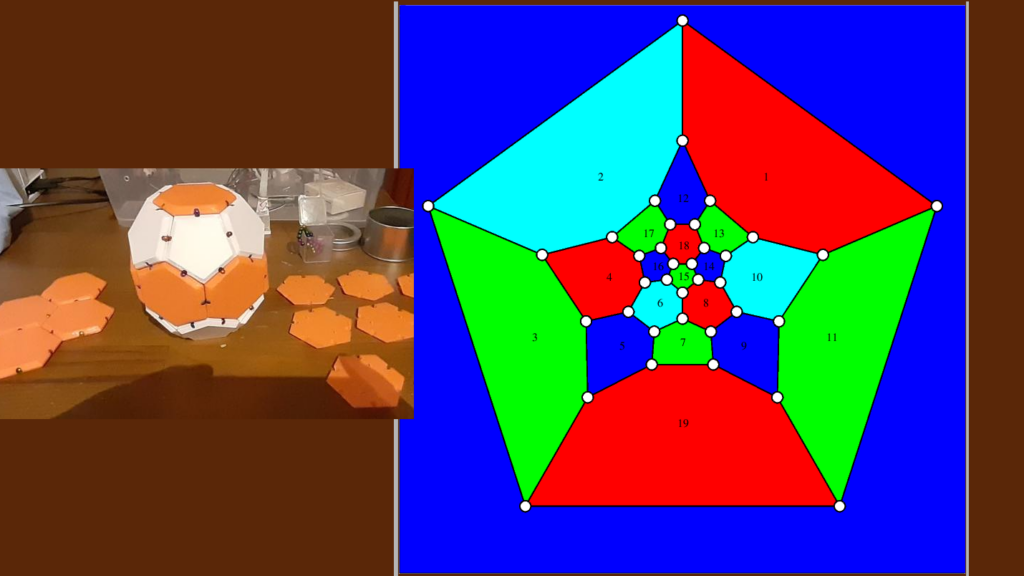
RE:
gdownton's "Polygons to Polyhedrons and More - 30mm Sides" models are very helpful, you can use the 12 pentagons and a subset of the 20 hexagons that build a C60 fullerene to build others. The shown ones are from this Raspberry forum thread posting onwards:
https://forums.raspberrypi.com/viewtopic.php?p=2011386#p2010195
C24:
C36.4, with 8-cycle of (orange) hexagons, photographed from two sides:
C36.14, with 3 connected components of pentagons only:
Finally I used this C40 planar embedding as instruction to build C40 from the polygons:
The two joining 5-rings of hexagons (1+2+4+6+8 and 11+10+14+13+12) were suspicious and so I built it:
As you can see, where the hexagon 5-rings join, only the magnets match, but not the sides.
There is simple reason for this planar embedding not being foldable with regular pentagons and hexagons:
3 hexagons joining with each angle of 120° sum up top 360° full circle.
That means all three hexagons have to stay in the same plane in 3D space.
I really need to get "node_fold_cubic.js" working, which tests for a planar embedding, whether it is foldable (nodejs script creates OpenSCAD 3D debug output):
RE:
I really need to get "node_fold_cubic.js" working, which tests for a planar embedding, whether it is foldable (nodejs script creates OpenSCAD 3D debug output):
Not needed anymore, yesterday I improved script might_be_foldable.js that does determine whether a fullerene embedding might be foldable (with regular pentagons and regular hexagons) by doing simple tests for all edges of the graph, in its dual graph:
https://forums.raspberrypi.com/viewtopic.php?p=2036410#p2036410
And the result of applying that script to all 30.5K non-isomorphic fullerenes with ≤100 vertices showed exactly two fullerenes that might be foldable:
C20.1 (regular dodecahedron)
C60.936 (=I60.1, football fullerene)
Those are known to be foldable from Wikipedia:

RE: Toothpick polyhedra, fullerenes
It's really awesome. This is an incredible invention in today's world.
RE:
I'm stunned to the core!